Link to paper: https://academic.oup.com/mnras/article/528/1/160/7492797
Internal shocks are ubiquitous in astrophysical scenarios where outflow has matter moving at variable speeds. The faster trailing material collides with the slower leading material leading to the formation of shocks. These shocks dissipate part of the kinetic energy of the material into internal energy. A fraction of the internal energy is then channeled into electromagnetic radiation for an underlying emission mechanism. Estimation of how efficiently the shocks dissipate energy is a necessary ingredient for application in any specific astrophysical scenarios. However, most works on internal shocks make use of ballistic approximation where plastic collision of two point-like masses is assumed. But realistic estimates of thermal efficiency require solving for the shock hydrodynamics post collision. In each collision two shock fronts are generated with different shock strengths and propagation velocities and internal energy dissipation rates. In this work we undertake such an exercise and find that there can be significant differences between the efficiency estimated from the ballistic approach and the hydrodynamic approach. This is especially important when the relative velocity of the colliding masses are high. At this limit, the ballistic approach suggests very high thermal efficiency. The hydrodynamic approach suggests otherwise. When one treats the hydrodynamics we need to take into account rarefaction waves which can catch up with either of the shock fronts and halt dissipation. The rarefaction waves are triggered effectively at high relative proper speeds and lead to partially shocked shells and hence the rapid drop in thermal efficiency (see Fig 1.) This important consideration needs to be taken in any analysis of an astrophysical scenario.
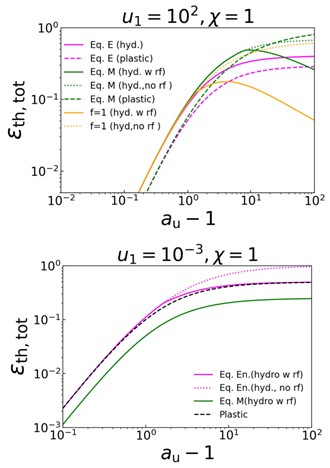
The figure compares the thermal efficiency from the ballistic (dashed curves) and the hydrodynamic approach (solid curves) as a function of the relative proper speed of the colliding objects. The upper and lower panel is for collision of bodies moving at relativistic and Newtonian speeds respectively. It can be seen that at very low speed contrast the hydrodynamic efficiency is higher than the ballistic efficiency while at very high proper speed contrast the hydrodynamic efficiency is much smaller due to rarefaction waves leading to partially shocked shells.