In collaboration with: A. A. Starobinsky (Landau Inst.) and D. Polarski (U. Montpellier)
Bouncing non-singular isotropic cosmological solutions are investigated in a simple model of scalar-tensor gravity. New families of such solutions are found and their properties are presented and analyzed using an effective potential as the main tool. Bouncing solutions are shown to exist for a Higgs-like self-interaction potential which is bounded from below, in contrast to previous solutions that appeared in the literature based on potentials which were unbounded from below. In the simplest version of a scalar field with the quartic potential and conformal coupling to gravity, bouncing spatially flat solutions either have the Hubble function diverging in the past before the bounce, but with a well-behaved future, or are globally regular but unstable with respect to anisotropic or inhomogeneous perturbations at some finite values of the scalar field and curvature. Regular solutions can only exist in the part of the parameter space where the maximum of the effective potential is larger than the first zero of the potential, and gravity becomes repulsive at the bounce.
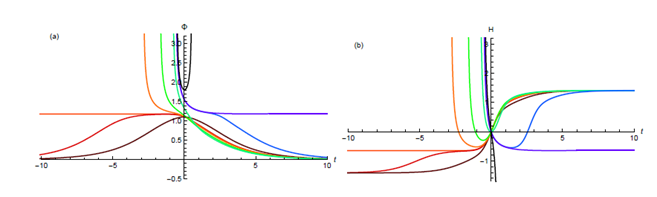
Several representative “time-profiles” (scalar field Φ(t) and Hubble function H(t)) of cosmological bounce solutions for the conformally coupled case (ξ=1/6). These bounce solutions violate the condition F(Φ)>0 at the bounce. Note that the symmetric Φ(t) solution has a maximum at the bounce. Note also a symmetric Φ(t) solution with a minimum at t=0. Bounce solutions are those that satisfy H(0)=0, H’(0)>0 and have no future singularities.
Reference:
Bouncing Cosmological Isotropic Solutions in Scalar-Tensor Gravity, D. Polarski, A.A. Starobinsky and Y. Verbin, JCAP 01 (2022) 052; e-Print: 2111.07319 [gr-qc]