Supposing that one is already familiar with special relativistic physics, what constitutes the best route via which to arrive at the architecture of the general theory of relativity? Although common wisdom, as well as the later Einstein, would stress the significance of mathematical and theoretical principles in answering this question, in this article we follow the lead of the earlier Einstein (circa 1916) and stress instead how one can go a long way to arriving at the general theory via inductive and empirical principles, without invoking presumptions concerning the geometrical structure of the final theory. We focus on the construction of the kinematical structure and the terms describing the coupling of matter to gravity.  General covariance, understood and employed as a straightforward extrapolation of empirical considerations, is central to our derivation, together with what we dub the `Methodological Equivalence Principle'. We argue that our approach has a number of virtues, both for one's understanding of the general theory of relativity, but also for pedagogy, since it stresses---to the greatest extent possible (a lesson which we inherit from John Bell's `How to teach special relativity', 1976)---both the methodological precedence of dynamical considerations to interpretative issues and the theoretical continuity between general relativity and its precursors. Riemannian geometry, according to this understanding, constitutes a possible interpretation of general relativity rather than an essential part of it. We conclude by comparing our approach to other philosophical approaches to general relativity and discussing the significance of empirically motivated methodological principles in the philosophy of science. Hetzroni, G. & Read, J. (2024) How to Teach General Relativity. The British Journal for the Philosophy of Science. (doi: 10.1086/729059; preprint)

In collaboration with: A. A. Starobinsky (Landau Inst.) and D. Polarski (U. Montpellier) Bouncing non-singular isotropic cosmological solutions are investigated in a simple model of scalar-tensor gravity. New families of such solutions are found and their properties are presented and analyzed using an effective potential as the main tool. Bouncing solutions are shown to exist for a Higgs-like self-interaction potential which is bounded from below, in contrast to previous solutions that appeared in the literature based on potentials which were unbounded from below. In the simplest version of a scalar field with the quartic potential and conformal coupling to gravity, bouncing spatially flat solutions either have the Hubble function diverging in the past before the bounce, but with a well-behaved future, or are globally regular but unstable with respect to anisotropic or inhomogeneous perturbations at some finite values of the scalar field and curvature. Regular solutions can only exist in the part of the parameter space where the maximum of the effective potential is larger than the first zero of the potential, and gravity becomes repulsive at the bounce. 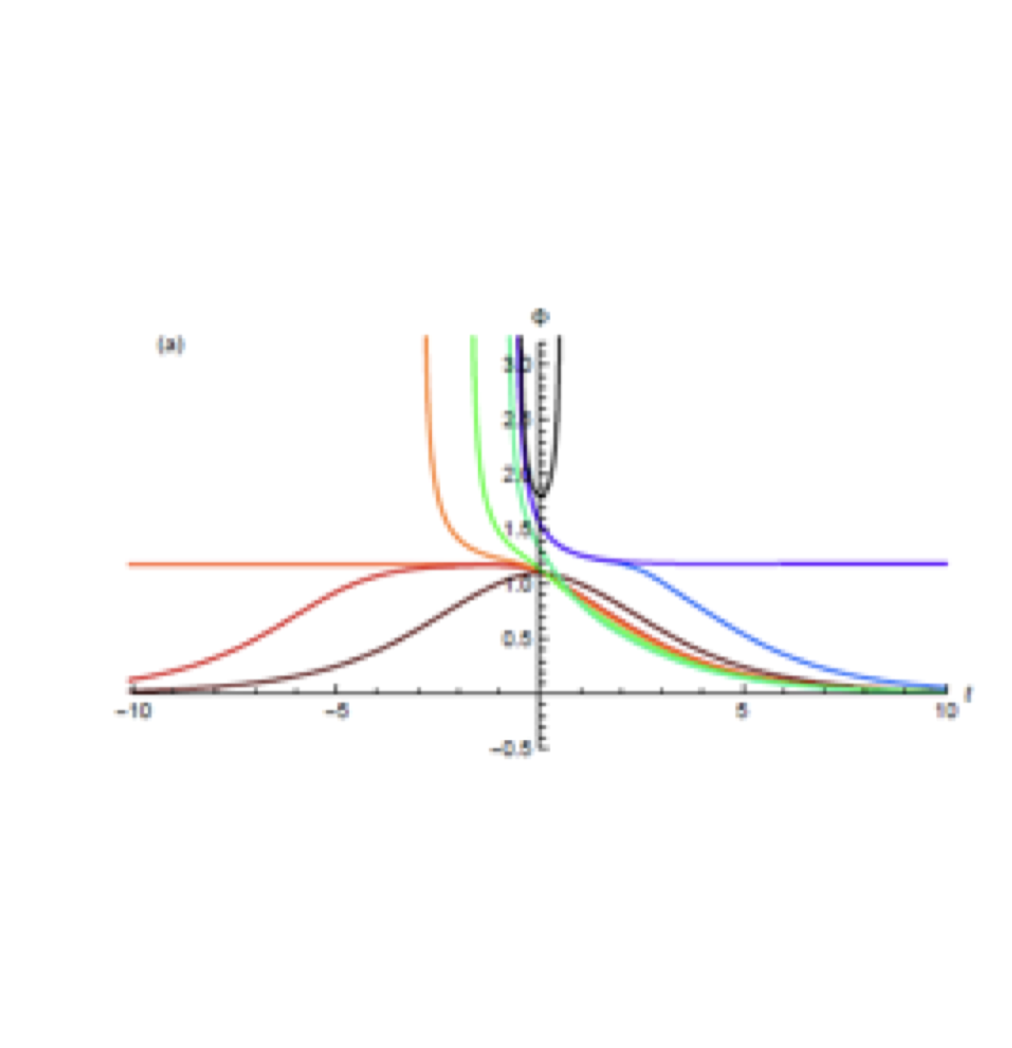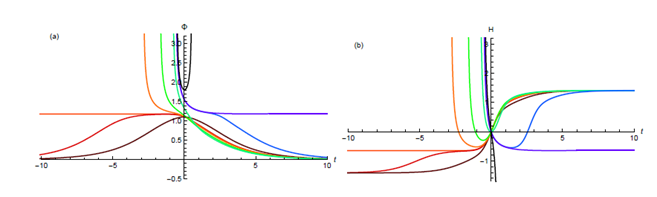Several representative “time-profiles” (scalar field Φ(t) and Hubble function H(t)) of cosmological bounce solutions for the conformally coupled case (ξ=1/6). These bounce solutions violate the condition F(Φ)>0 at the bounce. Note that the symmetric Φ(t) solution has a maximum at the bounce. Note also a symmetric Φ(t) solution with a minimum at t=0. Bounce solutions are those that satisfy H(0)=0, H’(0)>0 and have no future singularities. Reference: Bouncing Cosmological Isotropic Solutions in Scalar-Tensor Gravity, D. Polarski, A.A. Starobinsky and Y. Verbin, JCAP 01 (2022) 052;  e-Print: 2111.07319 [gr-qc]  

In collaboration with Y. Brihaye (Mons U) Study of the Horndeski-Reissner-Nordstrom black hole (HRNBH) solutions. The electric and magnetic types of these BHs differ from each other, since there is no duality symmetry between electric and magnetic fields in the vector-tensor Horndeski gravity. The magnetic black hole solutions are especially simple and can be written explicitly in terms of hypergeometric functions. It is natural to expect that these black holes undergo spontaneous scalarization and it is indeed the case, if we add a massless real scalar field which is coupled to the vector-tensor Horndeski term. The single coupling constant of the Horndeski term is promoted now to a scalar field-dependent coupling function. This system contains (ordinary) Reissner-Nordstrom black holes with a vanishing scalar field, but on a certain “bifurcation surface” in parameter space these solutions become unstable and scalarized HRNBHs appear. The “double-faced” solutions of dyonic scalarized BHs exist in a certain domain of parameter space which is bounded by a critical surface on which the nature of the limiting solutions is determined by the proximity to the lines of vanishing electric or magnetic charges. 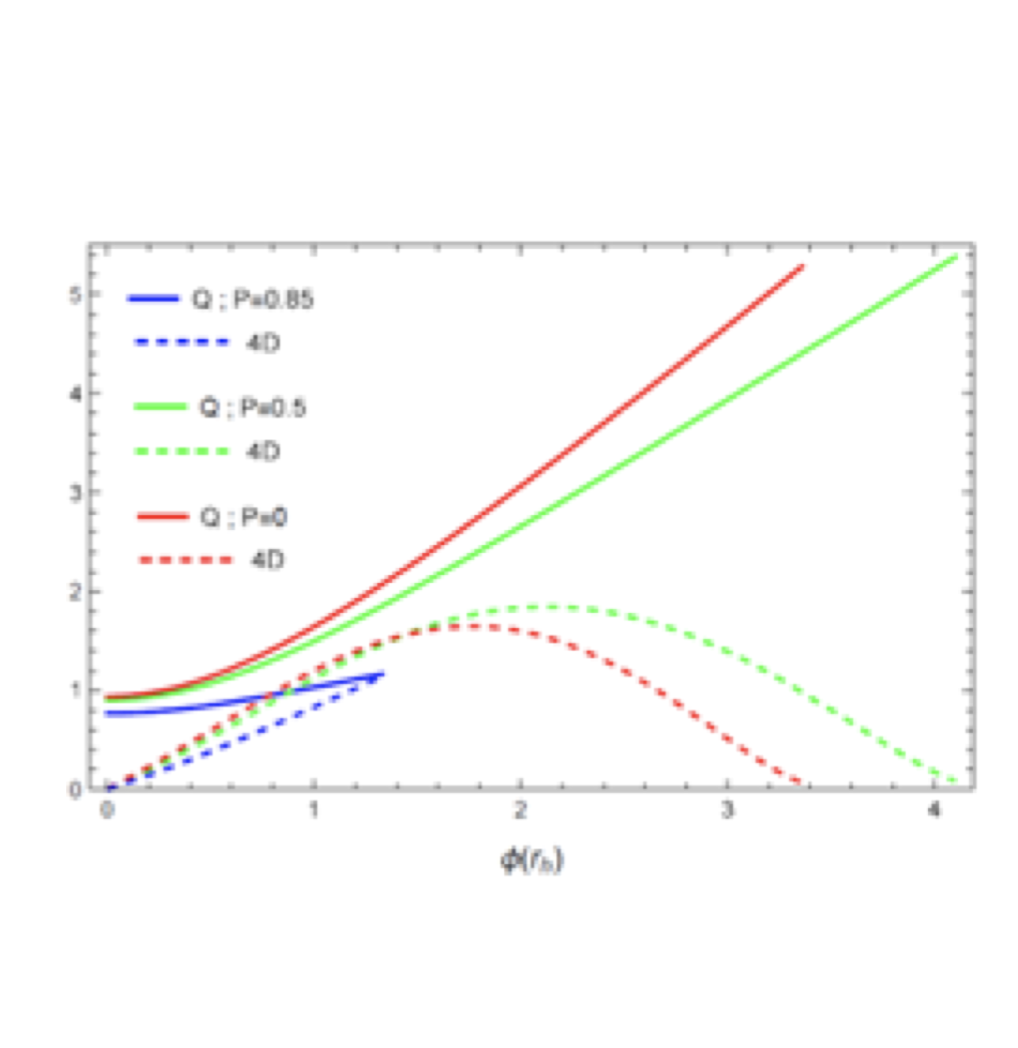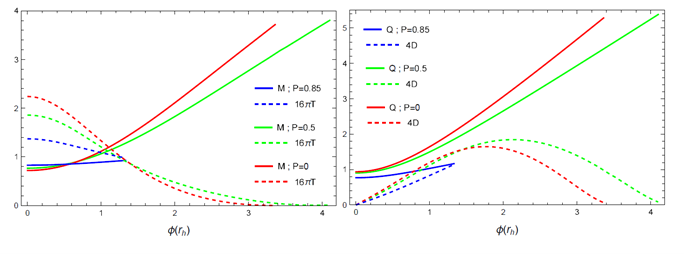The dependence on the horizon value of the scalar field of the: mass (M), electric charge (Q), scalar charge (D) and Hawking temperature (T) of scalarized Horndeski Black holes with magnetic charges P=0, 0.5, 0.85. Left: mass and temperature, Right: electric and scalar charges. References: Y. Brihaye and Y. Verbin, Scalarized compact objects in the vector-tensor Horndeski gravity, Phys. Rev. D102 124021 (2020). Y. Verbin, Magnetic black holes in the vector-tensor Horndeski theory, arXiv: 2011.02515. Y. Brihaye and Y. Verbin, Scalarized dyonic black holes in the vector-tensor Horndeski gravity, Phys. Rev. D104, 024047 (2021).